Gnu-Octave

Dinámica del sistema masa-resorte-amortiguador con ODE45.

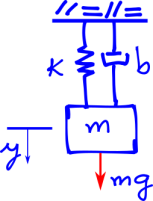
El siguiente ‘script’ muestra un sistema masa-resorte-amortiguador, resuelto con la función ODE45. Además, la fuerza ‘u’ externa puede ser considerada a través de la función fuerza().

function nonlinearModel()
to=0;    % start time
tf=20;   % end time
t=linspace(to,tf,100);
yo(1)=2; % initial condition
yo(2)=0;
[t,ydot] = ode45(@(t,y)nonlinear(t,y),t,yo);
plot(t,ydot)

function [ydot] = nonlinear(t,y)
% parameters
  k=1;
  b=1/2;
  m=1;
% proportional plus derivative control action
u=fuerza(t);
%u=0; % no control action
ydot=[y(2);
     - k/m*y(1) - b/m*y(2) + 1/m*u];
endfunction
function u=fuerza(t)
  u=1;
  %f=10;
  %u=sin(2*pi*f*t);
endfunction
endfunction

La figura resultante es, donde la linea azul corresponde a la posición y la linea roja corresponde a la velocidad.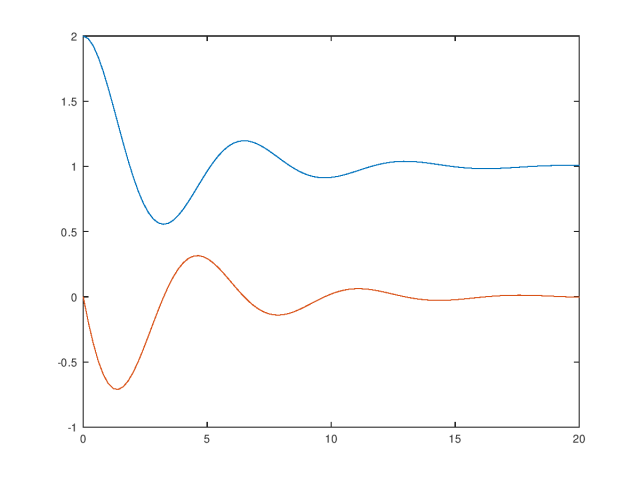

Vamos a suponer que la fuerza en el resorte es cuadrática respecto el desplazamiento. Por tanto se deberá sustituir el término – k/m*y(1) por – k/m*y(1)^2 , y ejecutar nuevamente el script. ODE45 estará resolviendo el modelo no lineal.

NOTA: el cambio de variable y1’=y1-mg/k fue realizado para trasladar el punto de equilibrio del sistema de (mg/k,0) para (0,0).